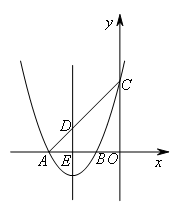
如图,已知抛物线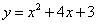 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,抛物线的对称轴交x轴于点E,连接CA,交抛物线的对称轴于点D.若抛物线上存在点M,使得直线CM把四边形DEOC分成面积相等的两部分,则点M的坐标为( )
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,抛物线的对称轴交x轴于点E,连接CA,交抛物线的对称轴于点D.若抛物线上存在点M,使得直线CM把四边形DEOC分成面积相等的两部分,则点M的坐标为( )
- A.
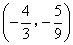
- B.
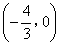
- C.
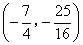
- D.
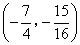
答案
正确答案:D
知识点:二次函数与几何综合
∵![]() ,
,
∴A(-3,0),B(-1,0),C(0,3).
抛物线的对称轴为直线![]() ,
,
∴△AOC和△ADE均为等腰直角三角形,
∴D(-2,1),
∴![]() .
.
如图,连接CE,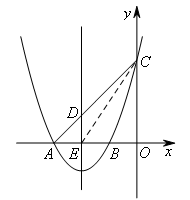
则![]() .
.
∵![]() ,
,
∴当直线CM把四边形DEOC分成面积相等的两部分时,
直线CM与x轴的交点F落在线段OE上,如图所示,
当![]() 时,得
时,得![]() ,
,
∴点![]() ,
,
∴直线CF:![]() ,
,
联立得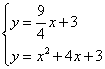 ,解得
,解得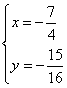 或
或![]() (舍),
(舍),
∴![]() .
.
略








