如图,在平面直角坐标系中放置一直角三角板,其顶点分别为A(0,1),
B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△COD.设点P是过C,D,B三点的抛物线上的一点,且在第一象限,若四边形PDCB的面积是△COD面积的4倍,则点P的坐标为( )
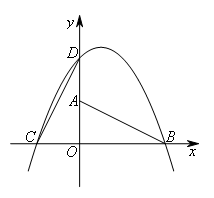
- A.
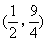
- B.
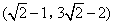
- C.
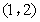
- D.
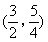
答案
正确答案:C
知识点:坐标系中的面积问题 铅垂法求面积 面积处理思路(割补法)
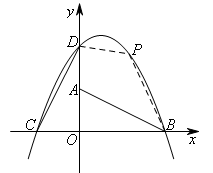
由题意得,C(-1,0),D(0,2),
过C,D,B三点的抛物线的解析式为![]() ,
,
如图,连接PD,PB,设点P的横坐标为m(![]() ).
).
易知![]() ,
,![]() ,
,
四边形PDAB中,A,D,B是定点,P是动点,
考虑将四边形PDAB分成△DAB和△PDB来计算.
如图所示,连接DB,过点P作PE∥y轴,交DB于点E.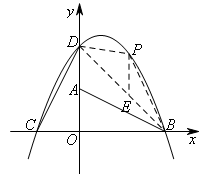
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
易知直线DB:![]() ,
,
∵点P的横坐标为m(![]() ),
),
∴点![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
解得![]() ,
,
即P点的横坐标为1,
∴点P(1,2).
略








