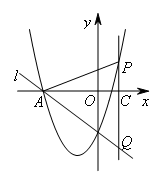
如图,已知直线 与x轴交于点A,点P是第一象限内抛物线
与x轴交于点A,点P是第一象限内抛物线 上的一个动点,过点P作y轴的平行线,交x轴于点C,交直线
上的一个动点,过点P作y轴的平行线,交x轴于点C,交直线 于点Q.若△APQ为等腰三角形,则点Q的坐标为( )
于点Q.若△APQ为等腰三角形,则点Q的坐标为( )
- A.

- B.

- C.
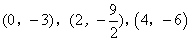
- D.
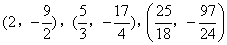
答案
正确答案:D
知识点:等腰三角形的存在性
1.解题要点
①首先分析基本图形,将信息进行标注;
②分析目标△APQ,A是定点,P,Q是动点,∠AQP大小不变,并不是常说的“夹角固定、两点动”,但两处有类似的地方:边可以表达,角度可以用来找相似;
③确定分类标准,表达,根据特征建等式.
2.解题过程
由题意得,A(-4,0),抛物线与x轴的另一交点为(1,0),
△ACQ是三边之比为3:4:5的直角三角形.
设点P的横坐标为t![]() ,
,
则![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
在Rt△ACQ中,AC=t+4,
∴![]() .
.
①当AP=AQ时,
∵PQ⊥AC,
∴PC=CQ,
∴![]() ,解得
,解得![]() .
.
∵![]() ,
,
∴![]() .
.
②当PQ=AQ时,![]() ,
,
解得![]() .
.
∵![]() ,
,
∴![]() .
.
③当AP=PQ时,如图,过点P作PE⊥AQ于点E.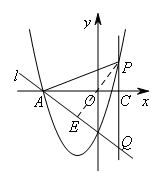
则![]() ,
,
易证△PEQ是三边之比为3:4:5的直角三角形,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
化简可得![]() ,
,
解得![]() .
.
∵![]() ,
,
∴![]() .
.
综上,点Q的坐标为![]() .
.
略








