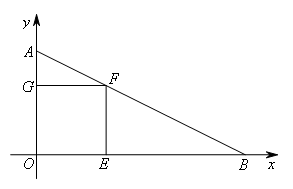
如图,在平面直角坐标系中,已知A(0,3),B(6,0).连接AB,E为线段OB上一点,以OE为边在第一象限内作正方形OEFG,其顶点F恰好落在线段AB上.将正方形OEFG沿OB向右平移,记平移中的正方形OEFG为正方形DEFG,正方形DEFG的边EF与AB交于点M,DG所在的直线与AB交于点N,
连接DM.设平移的距离为t ,当△DMN是等腰三角形时,t的值为( )
,当△DMN是等腰三角形时,t的值为( )
- A.
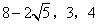
- B.
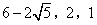
- C.
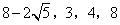
- D.
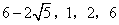
答案
正确答案:B
知识点:等腰三角形的存在性(三动点)
1.解题要点
①首先研究基本图形,△AOB是三边之比为![]() 的直角三角形,
的直角三角形,
正方形![]() 的边长为2,各线段长如图中标注所示,
的边长为2,各线段长如图中标注所示,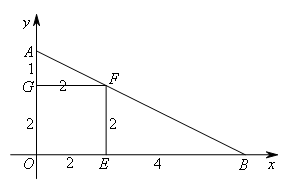
②分析运动状态,对起点,终点判断,能够得到当点E平移到点B时,运动停止.
③画出草图,如图所示,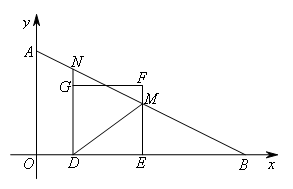
分析目标△DMN,D,M,N都是动点,属于等腰三角形的存在性(三点动)的情况,需要分析不变特征,表达边或角.
④无论怎么平移,正方形大小不变,△NDB和△MEB是三边之比为![]() 的直角三角形也不变,所以表达三边长,分别联立建等式求解.
的直角三角形也不变,所以表达三边长,分别联立建等式求解.
2.解题过程
由题意得,OD=t,DB=6-t,EB=4-t.
∵△AOB∽△NDB∽△MEB,
∴![]() ,
,
∴![]() .
.
在Rt△DEM中,DE=2,![]() ,
,
∴![]() .
.
如图,过点M作MH⊥ND于点H,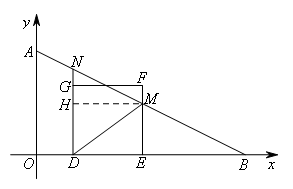
则四边形MHDE是矩形,△NHM是三边之比为![]() 的直角三角形.
的直角三角形.
∵MH=DE=2,
∴![]() .
.
①当MN=ND时,![]() ,
,
∴![]() ,符合题意.
,符合题意.
②当MN=DM时,![]() ,
,
解得![]() .
.
∵![]() ,
,
∴![]() .
.
③当DN=DM时,![]() ,
,
解得t=1,符合题意.
综上所述,符合题意的t的值为![]() .
.
略








