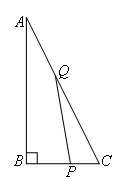
如图,在△ABC中,∠ABC=90°,AB=4,BC=2.P是线段BC上一动点,Q是线段AC上一动点,且始终满足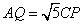 .当△CPQ是直角三角形时,CP的长为( )
.当△CPQ是直角三角形时,CP的长为( )
- A.0,2
- B.
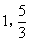
- C.
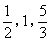
- D.
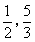
答案
正确答案:B
知识点:直角三角形的存在性
1.解题要点
①首先研究基本图形(三角形的边角性质);
②分析目标△CPQ,C是定点,P,Q是动点,若△CPQ是直角三角形,需要根据直角顶点进行分类,把三个顶点轮流作直角顶点进行分析;
③考虑分类时,从最简单的入手,可以结合题目背景进行分析排除,如点C不能作为直角
顶点.
2.解题过程
由题意得,![]() ,
,![]() .
.
①当∠CPQ=90°时,如图所示,
易证△CPQ∽△CBA,
∴![]() ,
,
∴CP=1,符合题意.
②当∠PQC=90°时,如图所示,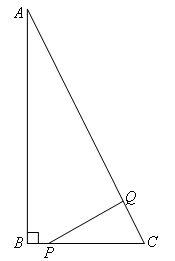
易证△CPQ∽△CAB,
∴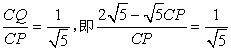 ,
,
∴![]() ,符合题意.
,符合题意.
综上所述,当△CPQ是直角三角形时,CP的长为![]() .
.
略








