如图,在矩形OABC中,OA=10,AB=8,点D在AB边上,沿直线CD折叠,使点B落在OA边上的点E处.分别以OC,OA所在直线为x轴、y轴建立平面直角坐标系,抛物线 经过O,D,C三点.点N在抛物线对称轴上,点M在抛物线上,当以M,N,C,E为顶点的四边形是以CE为边的平行四边形时,点M的坐标为( )
经过O,D,C三点.点N在抛物线对称轴上,点M在抛物线上,当以M,N,C,E为顶点的四边形是以CE为边的平行四边形时,点M的坐标为( )
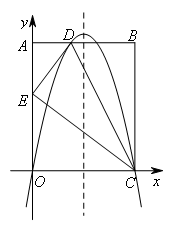
- A.
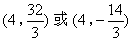
- B.

- C.
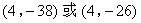
- D.
答案
正确答案:B
1.解题要点
在以M,N,C,E为顶点的四边形中,C,E为定点,M,N分别为抛物线和对称轴上的动点,从固定线段CE入手进行分析.
由于CE是平行四边形的边,故利用平移来处理问题.
2.解题过程
由折叠可知,BD=DE,CE=CB=10.
∵在Rt△EOC中,OC=AB=8,CE=10,
∴OE=6,
∴AE=4.
设AD=m,则DE=BD=8-m,
在Rt△ADE中,由勾股定理可得![]() ,
,
解得![]() ,即
,即![]() ,
,
∴D(3,10).
由O(0,0),C(8,0),D(3,10)可求得抛物线的解析式为![]() ,
,
∴抛物线的对称轴为直线x=4.
如图,MN∥CE且MN=CE.
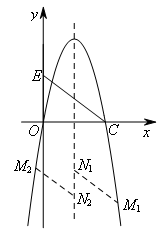
①当四边形![]() 是平行四边形时,
是平行四边形时,

∵点![]() 的横坐标为4,
的横坐标为4,
∴点![]() 的横坐标为12,
的横坐标为12,
∴![]() .
.
②当四边形![]() 是平行四边形时,
是平行四边形时,

∵点![]() 的横坐标为4,
的横坐标为4,
∴点![]() 的横坐标为-4,
的横坐标为-4,
∴![]() .
.
综上,满足题意的点M的坐标为![]() .
.
略








