如图,已知抛物线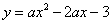 与x轴交于A,B两点(点A在点B左侧),过点A的直线交抛物线于另一点D(2,-3),且tan∠BAD=1.若点M在抛物线上,点N在x轴上,且以A,D,M,N为顶点的四边形是平行四边形,则点M的坐标为( )
与x轴交于A,B两点(点A在点B左侧),过点A的直线交抛物线于另一点D(2,-3),且tan∠BAD=1.若点M在抛物线上,点N在x轴上,且以A,D,M,N为顶点的四边形是平行四边形,则点M的坐标为( )
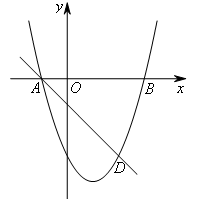
- A.
- B.
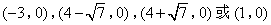
- C.
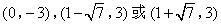
- D.
答案
正确答案:C
1.解题要点
①根据题目要求,确定为平行四边形存在性问题.
②分析定点、动点,挖掘不变特征.A,D为定点,M,N分别为抛物线和x轴上的动点,AD为定线段,把AD当作平行四边形的边或对角线来分类讨论.
③每种情况下,分析几何特征,画出图形,表达线段长,建等式求解.
2.解题过程
∵tan∠BAD=1,
∴![]() .
.
又∵点D的坐标为(2,-3),
∴直线AD的表达式为y=-x-1,
∴A(-1,0).
代入![]() 得,a=1,
得,a=1,
∴抛物线的表达式为![]() .
.
①如图,当AD为边时,
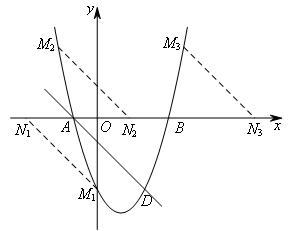
易得点![]() 的纵坐标为-3,点
的纵坐标为-3,点![]() 的纵坐标均为3,
的纵坐标均为3,
代入抛物线解析式可得![]() .
.
如图,当AD为对角线时,
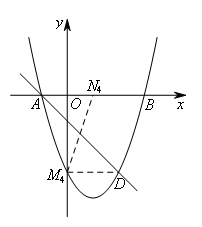
∵![]() ∥
∥![]() ,
,
∴点![]() 的纵坐标为3,
的纵坐标为3,
∴![]() .
.
综上,点M的坐标为![]() .
.
略








