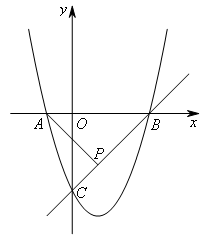
如图，抛物线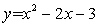与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，点P（1，k）在直线BC上．已知点M在x轴上，点N在抛物线上，若以A，M，N，P为顶点的四边形是平行四边形，则满足条件的点M有(    )个．

易求得A（-1，0），P（1，-2）．
A，P为定点，M，N分别为x轴和抛物线上的动点，要使得以A，M，N，P为顶点的四边形是平行四边形，需把线段AP当作平行四边形的边或者对角线进行分类讨论．
当AP为边时，如图，

平移AP使得线段两端点分别在抛物线和x轴上，
共有4种情况，对应的点M分别为．
当AP为对角线时，如图，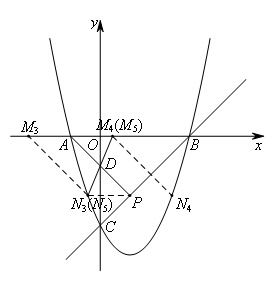

记AP与y轴的交点为D，易求得，D为线段AP的中点．
由点M在x轴上可知，此时PN∥x轴，点和点重合，
连接并延长，交x轴于点，
易证点与点重合（由于点P在对称轴上，故）．
综上可得，满足条件的点M有4个．

略