如图,在△ABC中,AB=AC=10cm,BC=8cm,D为AB的中点.点P在BC边上以3cm/s的速度由点B向点C运动;同时点Q在AC边上以相同的速度由点C向点A运动,其中一个点到达终点时另一个点也随之停止运动.当△BPD与△CQP全等时,点P运动的时间为( )
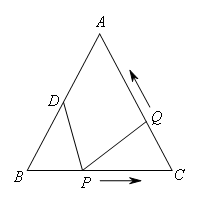
- A.
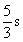
- B.
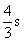
- C.
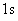
- D.
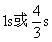
答案
正确答案:C
知识点:全等三角形的存在性
1.解题要点
①首先分析运动状态,设点P,Q的运动时间为ts.
分析运动过程: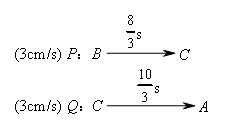
∴![]() .
.
对端点值进行验证:当t=0时,构不成△BPD,当![]() 时,构不成△CQP,故
时,构不成△CQP,故![]() .
.
②分析△BPD与△CQP,都是变化的三角形(只有点B,D,C是固定的),
∠B和∠C相等,已经有一组对应角(属于不变特征),
所以只要保证两夹边对应相等即可,此时需要分类讨论.
③求出结果之后,需要对答案进行验证.
2.解题过程
∵AB=AC,
∴∠B=∠C.
易得BP=3t,CQ=3t.
∵AB=10cm,BC=8cm,D为AB的中点,
∴BD=5cm,CP=(8-3t)cm.
①当△BDP≌△CPQ时,
BD=CP,BP=CQ,
即![]() ,
,
解得t=1,符合题意.
②当△BDP≌△CQP时,
BD=CQ,BP=CP,
即![]() ,
,
此方程组无解.
综上,当△BPD与△CQP全等时,点P运动的时间为1s.
略








