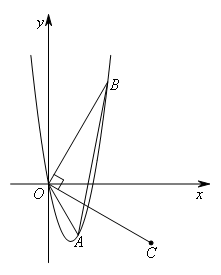
如图,已知点A,B在抛物线 上,点A在第四象限,点B在第一象限,且A,B两点的横坐标
上,点A在第四象限,点B在第一象限,且A,B两点的横坐标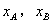 满足方程
满足方程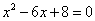 .连接OB,OA,AB,将线段OB绕点O顺时针
.连接OB,OA,AB,将线段OB绕点O顺时针
旋转90°得到线段OC.若D是坐标平面内一点,且△OAB和△OCD全等,则符合题意的点D的坐标为( )
- A.
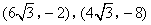
- B.
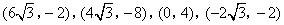
- C.
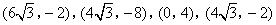
- D.
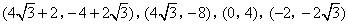
答案
正确答案:B
1.解题要点
①根据方程![]() ,结合抛物线可知点
,结合抛物线可知点![]() .
.
②分析基本图形,OB=8,OA=4,∠BOA=120°,![]() .
.
③在目标△OAB中,OB=8,OA=4,且∠BOA=120°,△OAB是固定的三角形.
△OCD中,OC=8,若△OAB和△OCD全等,需要保证:
∠OCD=120°,CD=4或∠COD=120°,OD=4.
2.解题过程
由题意得![]() ,
,
如图,过点B作BE⊥x轴于点E,过点A作AF⊥x轴于点F,过点C作CG⊥x轴于点G.
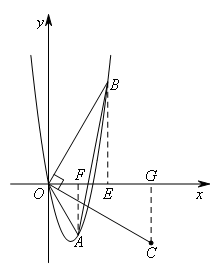
则∠BOE=60°,∠AOF=60°,
∴OB=8,OA=4,∠BOA=120°.
∵∠BOC=90°,
∴∠COG=30°.
∵OC=OB=8,
∴![]() .
.
①当∠OCD=120°,CD=4时,如图所示,
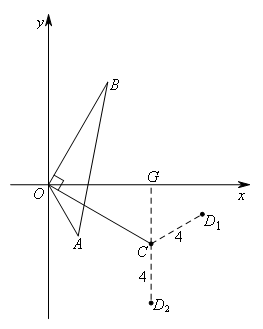
过点![]() 作
作![]() 于点H,各线段长如图所示,
于点H,各线段长如图所示,
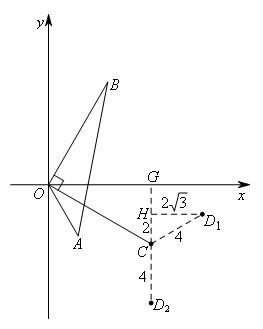
容易求得点![]() .
.
②当∠COD=120°,OD=4时,如图所示,
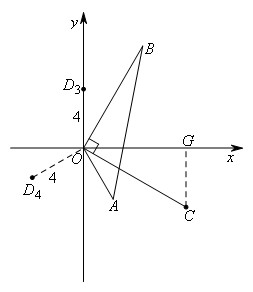
容易求得![]() .
.
综上所述,符合题意的点D的坐标为![]() .
.
略








