如图,抛物线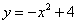 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,P是第一象限内抛物线上的一点,过点P作PD⊥x轴于点D,若△POD与△AOC相似,则点P的坐标为( )
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,P是第一象限内抛物线上的一点,过点P作PD⊥x轴于点D,若△POD与△AOC相似,则点P的坐标为( )
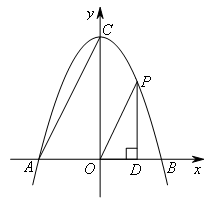
- A.
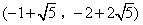
- B.
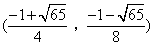
- C.
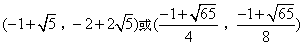
- D.
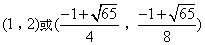
答案
正确答案:C
1.解题要点
①分析基本图形,OC=4,OA=2.
②研究目标△AOC,△AOC是两直角边之比为1:2的直角三角形;
△POD中,O是定点,PD⊥OD始终不变,若两个三角形相似,只需满足![]() 或
或![]() .
.
③坐标转线段长,利用比例关系建等式.
2.解题过程
由抛物线解析式可得A(-2,0),C(0,4),
∴△AOC是一个固定的直角三角形,且![]() .
.
△POD是一个动的直角三角形,若△POD与△AOC相似,
则只需满足![]() 或
或![]() .
.
设点P的横坐标为t(![]() ),则
),则![]() ,
,![]() .
.
①当![]() 时,解得
时,解得![]() 或
或![]() (舍),
(舍),
此时点P的坐标为![]() .
.
②当![]() 时,解得
时,解得![]() 或
或![]() (舍),
(舍),
此时点P的坐标为![]() .
.
综上,点P的坐标为![]() .
.
略








