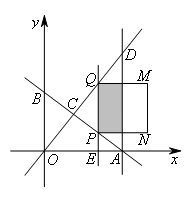如图,直线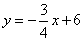 与x轴、y轴分别交于点A,B,直线
与x轴、y轴分别交于点A,B,直线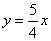 与AB交于点C,过点A且平行于y轴的直线交OC于点D.点E从点A出发,以每秒1个单位长度的速度沿x轴向左运动,过点E作x轴的垂线,分别交直线AB,OD于点P,Q,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E运动的时间为t(秒).
与AB交于点C,过点A且平行于y轴的直线交OC于点D.点E从点A出发,以每秒1个单位长度的速度沿x轴向左运动,过点E作x轴的垂线,分别交直线AB,OD于点P,Q,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E运动的时间为t(秒).
(1)当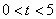 时,S与t之间的函数关系式为( )
时,S与t之间的函数关系式为( )
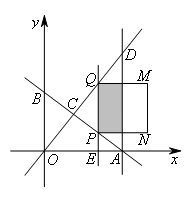
- A.
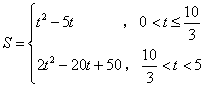
- B.
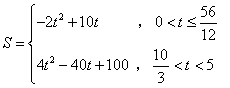
- C.
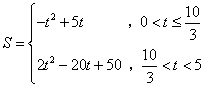
- D.
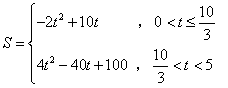
答案
正确答案:D
1.解题要点
①研究基本图形,求出点A,B,C,D的坐标.
②分析运动状态,背景图形△ACD不发生变化,正方形PQMN的大小发生变化.
当![]() 时,点E恰好在点C的正下方,即直线EQ过点C,
时,点E恰好在点C的正下方,即直线EQ过点C,
所以![]() 时间段的起点终点很容易判断.
时间段的起点终点很容易判断.
在正方形PQMN运动变化的过程中,边MN与△ACD会发生碰撞,MN会落在AD上,
所以运动状态为
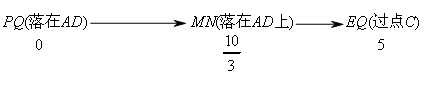
∴分两段,即![]() .
.
③分段画图,设计方案表达面积.
2.解题过程
由题意得,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
当边MN落在AD上时,如图所示,

此时PQ=PN=AE,
即![]() ,
,
解得![]() .
.
①当![]() 时,如图所示,
时,如图所示,
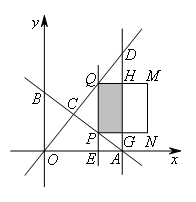
设MQ,PN分别与AD交于点H,G,
正方形PQMN与△ACD重叠部分为矩形PQHG.
∵![]() ,PG=AE=t,
,PG=AE=t,
∴![]() .
.
②当![]() 时,如图所示,
时,如图所示,

正方形PQMN落在三角形△ACD内,
∴![]() .
.
综上,当![]() 时,S与t之间的函数关系式为
时,S与t之间的函数关系式为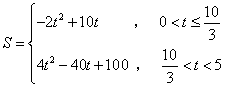 .
.
略