如图,在平面直角坐标系中,直线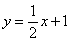 与抛物线
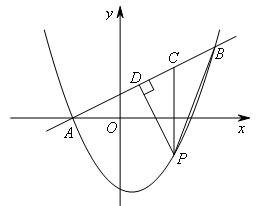
与抛物线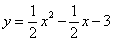 交于A,B两点,点A在x轴上,点P是直线AB下方的抛物线上一动点(不与点A,B重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.连接PB,线段PC把△PDB分成两个三角形.设点P的横坐标为m,则当m的值为( )时,这两个三角形的面积之比为9:10.
交于A,B两点,点A在x轴上,点P是直线AB下方的抛物线上一动点(不与点A,B重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.连接PB,线段PC把△PDB分成两个三角形.设点P的横坐标为m,则当m的值为( )时,这两个三角形的面积之比为9:10.
- A.
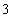
- B.
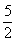
- C.
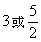
- D.
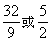
答案
正确答案:D
1.解题要点
①首先研究基本图形,求出点A,B的坐标;
利用点P的横坐标,可表达出点P,点C的坐标.
②研究目标中的两个三角形,属于背靠背模型,
若两个三角形的面积之比为9:10,只需满足![]() ;
;
也可以直接考虑有公共的底,只需要保证高之比满足题意即可.
③由于CD和BC都是坐标系中斜放置的线段,
所以利用坐标系中的处理原则,通过作横平竖直的线进行转化.
2.解题过程
联立直线与抛物线表达式,求得![]() ,
,![]() ,
,
∴![]() .
.
设PC与x轴交于点G,如图,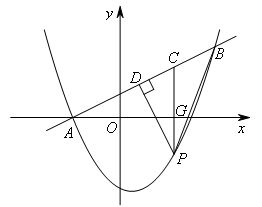
由直线AB的斜率为![]() 可知,△ACG是三边之比为
可知,△ACG是三边之比为![]() 的直角三角形,
的直角三角形,![]() .
.
分别过点D,B作PC的垂线,垂足分别为点E,F,如图所示,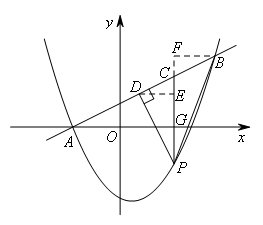
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
在Rt△CDP中,![]() ,
,
在Rt△DEP中,![]() ,
,
BF=4-m.
①![]() ,
,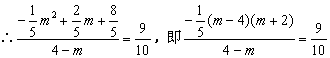 ,
,
解得![]() .
.
②![]() ,
,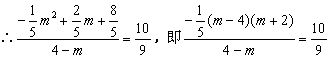 ,
,
解得![]() .
.
综上,符合题意的m的值为![]() .
.
略








