(上接第3题)(2)如图,将抛物线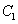 向下平移
向下平移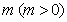 个单位,得到抛物线
个单位,得到抛物线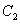 ,抛物线
,抛物线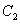 的顶点为P,交x轴负半轴于点M,交射线AB于点N,NQ⊥x轴于点Q.当NP平分∠MNQ时,m的值为( )
的顶点为P,交x轴负半轴于点M,交射线AB于点N,NQ⊥x轴于点Q.当NP平分∠MNQ时,m的值为( )
- A.1
- B.2
- C.
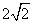
- D.2或
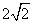
答案
正确答案:B
知识点:二次函数与几何综合 相似三角形的性质及判定 函数处理框架
由题意得,抛物线![]() 的解析式为
的解析式为![]() .
.
设点M的坐标为(t,0)(![]() ),则
),则![]() ,
,![]() ,
,
∴![]() ,
,
∴点P的坐标为![]() .
.
由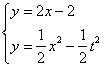 得,
得,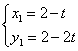 ,
,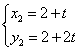 .
.
∴N(2-t,2-2t),
∴NQ=MQ=2-2t,
∴△MQN为等腰直角三角形.
如图,设MN交y轴于点G,过点N作NH⊥y轴于点H.
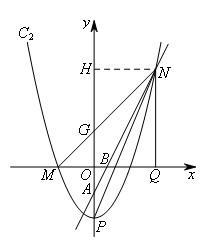
易得△MOG,△NHG均为等腰直角三角形,
∴OM=OG=-t,HG=NH=2-t,
∴![]() ,
,![]() .
.
∵PN平分∠MNQ,
∴∠MNP=∠PNQ.
∵NQ∥y轴,
∴∠NPG=∠PNQ,
∴∠MNP=∠NPG,
∴PG=NG,
即![]() ,
,
解得,![]() 或t=2(舍去),
或t=2(舍去),
∴![]() .
.
略








