如图,二次函数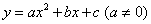 的图象与x轴交于点A(-3,0)和点B,与y轴交于点
的图象与x轴交于点A(-3,0)和点B,与y轴交于点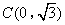 ,且当x=-4和x=2时二次函数的函数值相等.连接AC,BC.
,且当x=-4和x=2时二次函数的函数值相等.连接AC,BC.
(1)点M,N同时从点B出发,分别沿线段BA,BC运动,速度均为每秒1个单位长度,当其中一个点到达终点时,另一点也随之停止运动.设运动的时间为t秒,连接MN,将△BMN沿MN翻折.若点B恰好落在线段AC上的点P处,则点P的坐标为( )
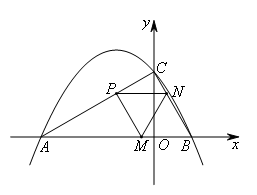
- A.
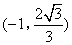
- B.
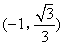
- C.
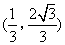
- D.
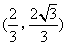
答案
正确答案:A
知识点:翻折变换(折叠问题) 二次函数与几何综合 函数处理框架
∵点![]() 在抛物线上,
在抛物线上,
∴![]() ,
,![]() .
.
∵当x=-4和x=2时二次函数的函数值相等,
∴抛物线的对称轴是直线x=-1.
可设抛物线的解析式为![]() ,
,
由A(-3,0),![]() 可得,
可得,![]() ,
,
∴B(1,0),OB=1,
∴BC=2,∠OBC=60°,∠OCB=30°.
在Rt△OAC中,OA=3,![]() ,
,
∴∠OAC=30°,∠OCA=60°,
∴∠ACB=90°.
由题意得,t的取值范围是![]() ,BN=BM=t,CN=2-t,
,BN=BM=t,CN=2-t,
∴△BMN为等边三角形,∠OBC=∠BMN=∠BNM=60°.
由折叠可知,BN=PN=BM=PM= t,∠PMN=∠PNM=60°,
∴∠CNP=∠PMA=60°.
在Rt△CPN中,∵∠CNP=60°,
∴NP=2CN,即t=2(2-t),
∴![]() .
.
如图,过点P作PD⊥x轴于点D.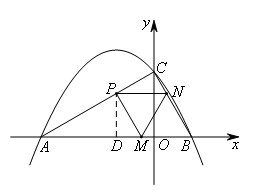
易得![]() ,
,![]() ,
,
∴![]() ,
,
∴点P的坐标为![]() .
.
略








