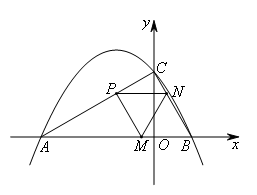
(上接第1题)在(1)的条件下,若二次函数图象的对称轴上存在点Q,使得以B,N,Q为项点的三角形与△ABC相似,则相应的t的值为( )
- A.
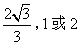
- B.
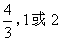
- C.
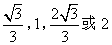
- D.
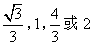
答案
正确答案:B
知识点:翻折变换(折叠问题) 二次函数与几何综合 函数处理框架
由(1)可知,△ABC是含30°角的直角三角形.
要使得以B,N,Q为项点的三角形与△ABC相似,则需△BNQ为直角三角形.
①当点B为直角顶点时,
如图,过点B作BN的垂线,与抛物线对称轴的交点即为点Q.
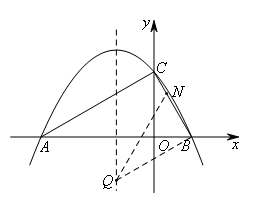
易求得点Q的坐标为![]() ,
,![]() .
.
当∠BQN=30°时,![]() ,
,![]() .
.
当∠BQN=60°时,点N落在抛物线对称轴上,不符合题意.
②当点N为直角顶点时,
如图,若∠QBN=60°,
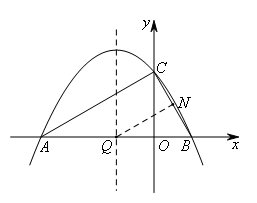
则点Q为抛物线对称轴与x轴的交点,此时点Q的坐标为(-1,0),
QB=2,BN=1,t=1.
如图,若∠QBN=30°,
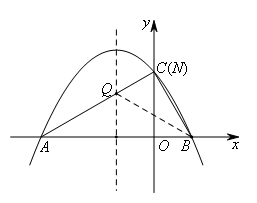
易求得点N与点C重合,BN=2,t=2.
③当点Q为直角顶点时,
如图,易证以BC为直径的圆与抛物线对称轴无交点,
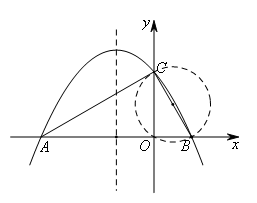
故不存在点Q为直角顶点的情况.
综上得,t的值为![]() .
.
略








