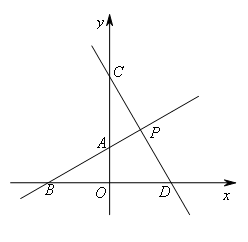
如图,直线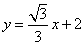 与坐标轴分别交于A,B两点,点C在y轴上,且
与坐标轴分别交于A,B两点,点C在y轴上,且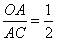 ,直线CD⊥AB于点P,交x轴于点D.若M为坐标系内一点,且以B,P,C,M为顶点的四边形是平行四边形,则点M的坐标为( )
,直线CD⊥AB于点P,交x轴于点D.若M为坐标系内一点,且以B,P,C,M为顶点的四边形是平行四边形,则点M的坐标为( )
- A.
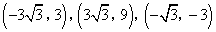
- B.
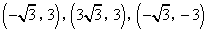
- C.
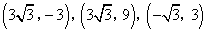
- D.
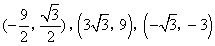
答案
正确答案:A
知识点:平行四边形的存在性
点击学习解析视频:http://v.xxt.cn/course/video.do?id=12582&ids=12582
1.解题要点
①首先研究基本图形,求出各点坐标,点P的坐标可通过两直线表达式联立求出.
②分析以B,P,C,M为顶点的四边形,B,P,C为定点,M为动点,符合平行四边形的存在性中三定一动的特征,分类时可以任意两边作邻边来构造平行四边形.
③分类画图,借助对边平行且相等,利用平移求出各点坐标.
2.解题过程
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵AB⊥CD,
∴![]() ,
,
∴![]() .
.
联立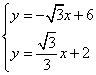 ,解得
,解得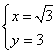 ,
,
∴![]() .
.
如图,连接BC,
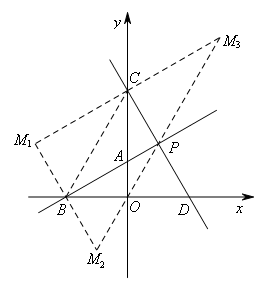
在△PCB中,分别过B,C,P三点,作对边的平行线,
三条直线的交点分别为![]() ,
,
此时四边形![]() ,四边形
,四边形![]() ,四边形
,四边形![]() 均为平行四边形.
均为平行四边形.
在平行四边形![]() 中,由平移可知,
中,由平移可知,
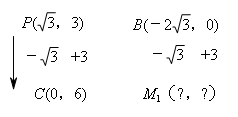
解得![]() ,
,
类比可求得![]() .
.
综上,符合题意的点P的坐标为![]() .
.
略








