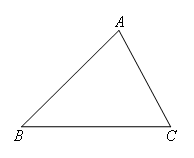
已知：如图，△ABC．求证：∠A+∠B+∠C=180°．

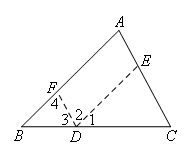
证明：如图，在BC上任取一点D，过点D作DE∥AB交AC于点E，作DF∥AC交AB于点F．

∵DE∥AB（辅助线的作法）
∴∠1=∠B（两直线平行，同位角相等）
∠2=∠4（                    ）
∵DF∥AC（辅助线的作法）
∴∠3=      ，∠A=∠4（两直线平行，同位角相等）
∴∠2=∠A（等量代换）
∵∠1+∠2+∠3=180°（                    ）
∴∠A+∠B+∠C=180°（等量代换）
①两直线平行，内错角相等；②两直线平行，同位角相等；③内错角相等，两直线平行；④∠DEA；
⑤∠DEC；⑥∠C；⑦平角的定义；⑧三角形的内角和是180°．
以上空缺处依次所填正确的是(    )

• A.③⑥⑧
• B.①④⑦
• C.②⑤⑦
• D.①⑥⑦

答案

正确答案：D

知识点：平行线的性质  三角形内角和  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>