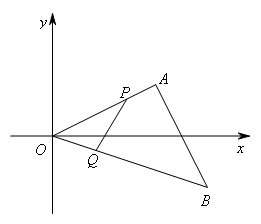
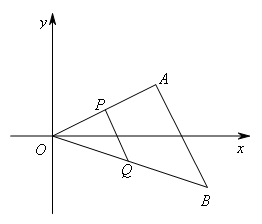
如图,在平面直角坐标系中,△AOB的三个顶点坐标分别为O(0,0),A(4,2),
B(6,-2),动点P从点A出发,以每秒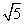 个单位长度的速度向点O运动,动点Q同时从点O出发,以每秒
个单位长度的速度向点O运动,动点Q同时从点O出发,以每秒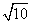 个单位长度的速度向点B运动,当其中一点到达终点时,另一点也随之停止运动.设运动的时间为t秒,当△OPQ为等腰三角形时,t的值为( )
个单位长度的速度向点B运动,当其中一点到达终点时,另一点也随之停止运动.设运动的时间为t秒,当△OPQ为等腰三角形时,t的值为( )
- A.
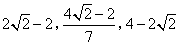
- B.
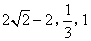
- C.
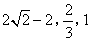
- D.
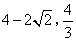
答案
正确答案:C
点击查看解析视频:http://v.xxt.cn/course/video.do?id=12624
1.解题要点
①理解题意,整合信息.
∵![]() ,
,
∴![]() .
.
△AOB的三个顶点坐标固定,可以通过解直角三角形来研究△AOB,
这里采用验证△AOB是等腰直角三角形的方式来说明.
如图,过点A作AD⊥y轴于点D,过点B作BC⊥AD于点C.
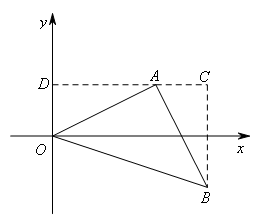
∵![]() ,
,
∴OD=2,AD=4,AC=2,BC=4,
∴△AOD≌△BAC,
∴OA=AB,∠OAB=90°,
∴∠AOB=45°.
如图,有同学会发现![]() 满足
满足![]() ,
,
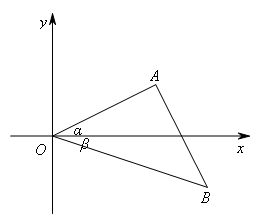
∴∠AOB=45°.
研究动点运动状态:
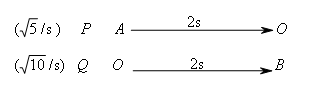
②抓不变特征有序思考,设计方案.
分析定点,动点,不变特征:
△OPQ中,P,Q是动点,O是定点,
在P,Q位置变化的过程中,∠POQ=45°不发生变化,属于不变特征;
确定分类标准:
分别利用三边两两相等,借助三线合一解决问题.
③根据方案作出图形,有序操作.
当OP=OQ时,直接表达线段长,利用线段长相等建等式;
当OP=PQ或OQ=PQ时,过顶角顶点作三线合一的线,表达线段长,利用线段间关系建等式.
④结果检验,总结.
作图验证,根据图形对结果进行判断;分析数据,对结果进行验证取舍.
2.解题过程
如图,过点A作AD⊥y轴于点D,过点B作BC⊥AD于点C.

∵![]() ,
,
∴OD=2,AD=4,AC=2,BC=4,
∴△AOD≌△BAC,
∴OA=AB,∠OAB=90°,
∴∠AOB=45°.
由题意得![]() ,
,
∴![]() .
.
①当OP=OQ时,如图所示,
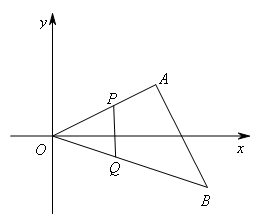
则![]() ,解得
,解得![]() ,符合题意.
,符合题意.
②当OQ=PQ时,如图所示,
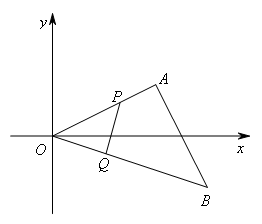
△OPQ是等腰直角三角形,
∴![]() ,
,
∴![]() ,解得
,解得![]() ,符合题意.
,符合题意.
③当OP=PQ时,如图所示,
△OPQ是等腰直角三角形,
∴![]() ,
,
∴![]() ,解得
,解得![]() ,符合题意.
,符合题意.
综上,符合题意的t的值为![]() .
.
略








