在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一块直角三角板的直角顶点放在点M处,并将此三角板绕点M旋转,三角板的两直角边与边OP,OQ分别交于点A,B,连接AB.则在旋转三角板的过程中,△AOB周长的最小值为( )

- A.

- B.
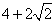
- C.6
- D.
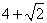
答案
正确答案:B
1.解题要点
要求△AOB周长的最小值,由于三边都是动线段,不容易直接进行表达,
考虑将线段进行转化,尽量减少变量.
由于M是斜边PQ的中点,可以利用斜边中线等于斜边一半;
或利用∠AMB是斜直角,考虑将斜直角转正.
这里采用前面一种方式来求解.
2.解题过程
如图,连接OM.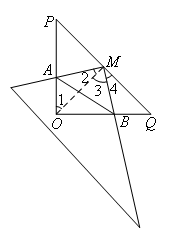
在等腰直角三角形POQ中,
∵M是PQ的中点,
∴OM⊥PQ,OM=MQ,∠1=∠Q=45°.
∵∠2+∠3=90°,∠3+∠4=90°,
∴∠2=∠4,
∴△AOM≌△BQM,
∴AO=BQ,AM=BM,
∴AO+OB=OQ=4,△AMB是等腰直角三角形,
∴![]() ,
,
∴![]() .
.
∵M是定点,A是定线段OP上一点,
∴当MA⊥OP时,AM的长度最小,如图所示,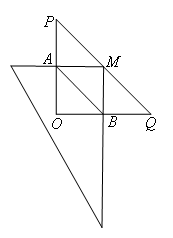
此时![]() ,
,
∴![]() .
.
略








