如图,在等腰直角三角形ABC中,AC=BC,∠ACB=90°,D,E是AB边上的两点,
且AD=6,BE=8,∠DCE=45°,则DE的长为( )
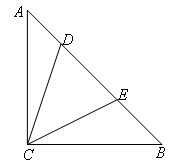
- A.14
- B.9
- C.10
- D.11
答案
正确答案:C
1.解题要点
题干当中提供了AC=BC这样一个等腰结构,就提供了一个旋转的可能,
进而就可以把条件整合在一起,
所以在求DE的时候,我们就可以利用旋转△ADC,
使得AC与BC重合,把条件整合到一起.
由于旋转只是一种思想,描述辅助线时,需要换成等价的描述方式.
2.解题过程
如图,过点C作CF⊥CD,使得CF=CD,连接BF,EF.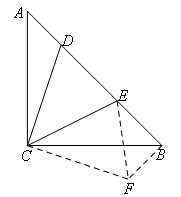
易得△ACD≌△BCF(SAS),
∴AD=BF=6,∠CAD=∠CBF=45°.
∵∠ACD+∠ECB=45°,
∴∠FCE=∠BCF+∠ECB=45°(∠BCF=∠ACD可由同角的余角相等得到),
∴∠DCE=∠FCE.
∵CD=CF,CE=CE,
∴△DCE≌FCE,
∴DE=EF.
∵∠EBF=∠EBC+∠CBF=45°+45°=90°,BF=6,BE=8,
∴EF=10,
∴DE=10.
略








