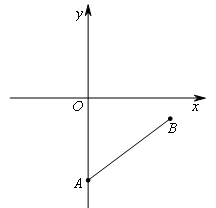
如图，已知A（0，-8），B（8，-2），P是坐标轴上一点，若△ABP是直角三角形，则符合题意的点P有(    )

1．解题要点
①理解题意，整合信息．
将坐标信息标注在图上．
②分析特征有序思考，设计方案．
分析定点，动点：△ABP中，A，B是定点，P是动点；
确定分类标准：以三角形的三个顶点轮流当直角顶点进行分类讨论．
③根据方案作出图形，有序操作．
当定点A或B为直角顶点时，由于AB是定直线，可以利用，
通过直线与坐标轴的交点来判断点的个数；
当动点P为直角顶点时，以AB为直径作圆，通过圆与坐标轴的交点来判断点的个数．
在判断位置关系时调用圆与直线的位置关系的处理手段．
④结果检验，总结．
作图验证，根据图形对结果进行判断；分析数据，对结果进行验证取舍．
2．解题过程
当∠PAB=90°时，过点A作直线，交x轴于点；
当∠PBA=90°时，过点B作直线，交x轴于点，交y轴于点．
如图所示，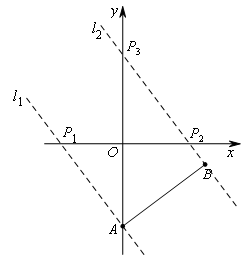

当∠APB=90°时，以AB为直径作⊙O′，如图所示，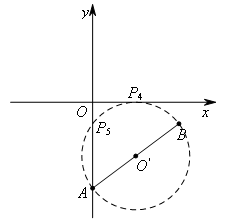

⊙O′与x轴相切，即只有一个交点；
与y轴相交，一个交点为A，记另一个交点为.
下面证明“⊙O′与x轴相切”．
如图，过点作轴于点D．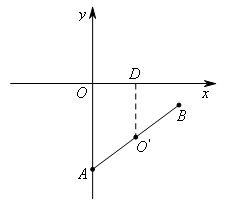

∵A（0，-8），B（8，-2），
∴，
∴，即，
∴⊙O′与x轴相切．
综上，符合题意的点P有5个．

略