问题背景
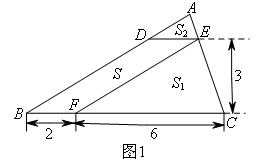
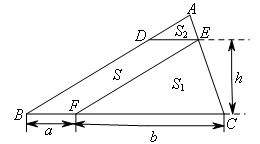
如图1,在△ABC中,D,E分别是边AB,AC上的点,且DE∥BC,过点E作EF∥AB,交BC于点F.
记四边形BFED的面积为S,△EFC的面积为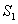 ,△ADE的面积为
,△ADE的面积为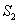 ,按图示数据能够得到
,按图示数据能够得到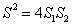 .
.
探究发现
(1)若BF=a,FC=b,DE与BC间的距离为h,其他条件不变,则 三者之间的关系满足( )
三者之间的关系满足( )
- A.
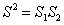
- B.
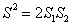
- C.
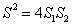
- D.
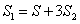
答案
正确答案:C
知识点:中考数学几何中的类比探究
点击查看解析视频:http://v.xxt.cn/course/video.do?id=13027
1.解题要点
①首先弄清楚在原数据下,图1中的结论是怎样得到的.
根据图形可知,![]() ,
,
由题意得四边形BFED是平行四边形,△ADE∽△EFC,
∴DE=BF=2,![]() ,
,
∴![]() ,
,
∴![]() ,
,
可以得到![]() .
.
我们是通过分别表达3个三角形的面积,最后进行验证的方式来说明的.
②当条件发生变化时,同样采取上述方式,先表达出各个面积,再研究他们之间的关系.
2.解题过程
如图,
∵DE//BC,EF//AB,
∴四边形BFED是平行四边形,∠AED=∠ECF,∠ADE=∠ABC=∠EFC,
∴DE=BF=a,△ADE∽△EFC.
由题意得![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() 三者之间的关系满足
三者之间的关系满足![]() .
.
略








