（上接第4题）拓展迁移
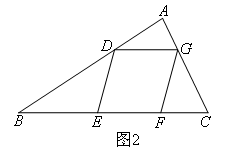
（2）如图2，平行四边形DEFG的四个顶点在△ABC的三边上，若△ADG，△DBE，△GFC的面积分别为2，5，3，利用（1）中的结论可以求出△ABC的面积为(    )

点击查看解析视频：http://v.xxt.cn/course/video.do?id=13027
1．解题要点
①要利用（1）中的结论，需要构造与（1）中相同的图形．
观察发现，要构造与（1）中相同的图形，只需要过点G作GH∥AB，交BC于点H，
此时的位置如图所示，满足．

②若要求△ABC的面积，根据，
只需要知道的面积即可，也即求出即可．
③根据四边形DBHG和四边形DEFG都是平行四边形，能够得到△DBE≌△GHF，
∴．
④
．
2．解题过程
如图，过点G作GH∥AB，交BC于点H，
此时的位置如图所示，满足．

∵四边形DEFG是平行四边形，
∴DG//BC，DE=GF，DG=EF．
∵GH//AB，
∴四边形DBHG是平行四边形，
∴DB=GH，DG=BH，
∴BH=EF，
∴BE=HF，
∴△DBE≌△GHF（SSS）．

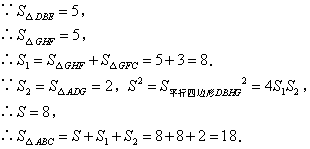
略