在矩形ABCD中,E是BC的中点,F在BC的延长线上,连接AE,过点E作EM⊥AE,交∠DCF的平分线于点M.如图1,当AB=BC时,能够得到AE=EM.
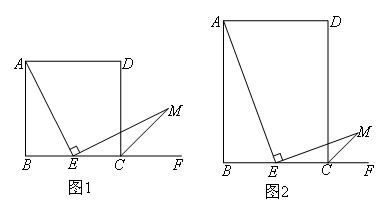
(1)如图2,当AB=nBC时,AE和EM之间的数量关系为( )
- A.
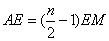
- B.
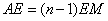
- C.
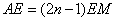
- D.

答案
正确答案:C
知识点:中考数学几何中的类比探究
点击查看解析视频:http://v.xxt.cn/course/video.do?id=13050
图1中的证明思路:
如图,在AB上截取BN=BE.
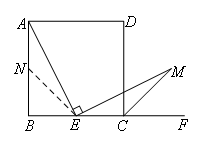
在正方形ABCD中,∠B=∠BCD=90°,AB=BC,
∴∠BNE=45°,
∴∠ANE=135°.
∵BE=EC,
∴AN=EC.
∵CM平分∠DCF,
∴∠DCM=45°,
∴∠ECM=∠ANE=135°.
∵EM⊥AE,
∴∠AEB+∠CEM=90°.
∵∠NAE+∠AEB=90°,
∴∠NAE=∠CEM,
∴△ANE≌△ECM,
∴AE=EM.
图2中的证明思路:
如图,在AB上截取BN=BE.
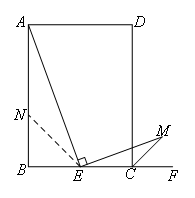
在矩形ABCD中,∠B=∠BCD=90°,AB=nBC,
∴∠BNE=45°,
∴∠ANE=135°.
设BE=EC=BN=a,则AB=2na,
∴AN=(2n-1)a.
∵CM平分∠DCF,
∴∠DCM=45°,
∴∠ECM=∠ANE=135°.
∵EM⊥AE,
∴∠AEB+∠CEM=90°.
∵∠NAE+∠AEB=90°,
∴∠NAE=∠CEM,
∴△ANE∽△ECM,
∴![]() ,
,
∴![]() .
.
略








