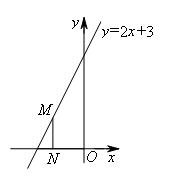如图,M是直线y=2x+3上的动点,过点M作MN⊥x轴于点N,则在y轴上是否存在点P,使△MNP为等腰直角三角形?小明发现:当动点M运动到(-1,1)时,y轴上存在点P(0,1),此时有MN=MP,△MNP为等腰直角三角形.在y轴上是否还存在符合条件的点P?请你写出其他符合条件的点P的坐标 .
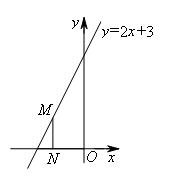
- A.
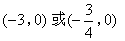
- B.
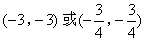
- C.
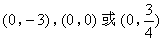
- D.
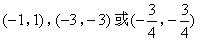
答案
正确答案:C
知识点:等腰直角三角形的存在性
由题意得,要使△MNP为等腰直角三角形,M,N,P三点均可作为直角顶点.
①如图,当∠NMP=90°时,
MN=MP,
设M(m,2m+3),则P(0,2m+3),N(m,0),
∴MN=|2m+3|,MP=|m|.
由|2m+3|=|m|得,m=-3或m=-1,
此时点P的坐标为(0,-3)或(0,1)(与已知点重合).
②如图,当∠MNP=90°时,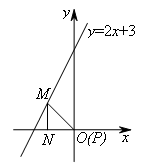
P为坐标原点,此时点P的坐标为(0,0).
③如图,当∠MPN=90°时,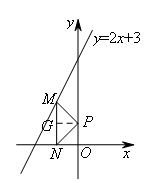
过点P作PG⊥MN于点G,则![]() .
.
设M(m,2m+3),则![]() ,MN=|2m+3|,PG=|m|.
,MN=|2m+3|,PG=|m|.
由![]() 得,
得,![]() ,
,
∴![]() ,即此时点P的坐标为
,即此时点P的坐标为![]() .
.
综上得,其他符合条件的点P的坐标为![]() .
.
略