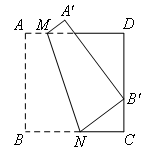
如图，四边形ABCD是边长为9的正方形纸片，将该纸片折叠，使点B落在CD边上的点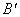处，点A的对应点为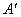，折痕为MN．若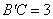，则AM的长为          ．

1．解题要点
①考虑折叠是全等变换，，若在直角三角形中求解，条件不全，所以考虑折叠的第二个层次．
第二层轴对称的性质：对称轴上任意一点到对应点的距离相等，所以连接，
则，通过勾股定理表达出两线段的长建等式．

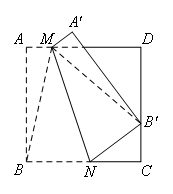
②考虑折叠是全等变换，可以求出，
轴对称会产生垂直平分线，连接，则，
过点M作ME⊥BC于点E，则，
可以求得EN的长，进而求得AM的长．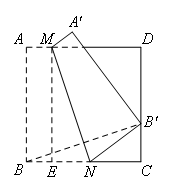

2．解题过程
方法一：如图，连接．

由折叠可知，，
在正方形ABCD中，∠A=∠D=90°，AB=AD=DC=9．
∵，
∴．
在Rt△MAB中，，
在中，，
∴，
解得AM=2．
方法二：如图，连接，过点M作ME⊥BC于点E．

四边形ABEM是矩形，ME=AB=9，AM=BE，
由折叠可知，，
在正方形ABCD中，，
在中，，
∴．
∵，ME=BC=9，
∴，
∴EN=3，
∴AM=BE=2．

略