如图，以△ABC的三边为边在BC同侧分别作三个正三角形，
即△ABD，△BCE，△ACF．（空白处填对应选项前的数字）

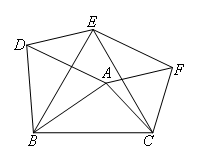
（1）四边形ADEF为____；
（1．平行四边形；2．菱形；3．矩形；4．一般的四边形）
（2）当△ABC满足条件____时，四边形ADEF为矩形；
（1．∠BAC=90°；2．∠BAC=120°；3．∠BAC=135°；4．∠BAC=150°）
（3）当△ABC满足条件____时，四边形ADEF为菱形；
（1．AB=AC；2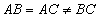．；3．AB⊥AC；4．∠BAC=150°）
（4）当△ABC满足条件____时，四边形ADEF不存在．
（1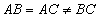．；2．AB=AC=BC；3．∠AB⊥AC；4．∠BAC=150°）

答案

1,4,2,2

知识点：存在性问题  平行四边形及特殊平行四边形性质、判定  

（1）由△DBE≌△ABC，△FEC≌△ABC，
可得DE=AC=AF，EF=AB=AD．
故四边形ADEF为平行四边形．
（2）由（1）四边形ADEF为平行四边形．
若四边形ADEF为矩形，
则∠DAF=90°．又因∠BAD=∠CAF=60°，
故∠BAC=90°．
（3）若四边形ADEF为菱形，
则AD=AF，且∠DAF<180°．
对比四个选项，可得AB=ACBC．
（4）当AB=AC=AC时，∠DAF=180°．
此时四边形ADEF不存在．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>