如图.在直角坐标系中.抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1,0)、B(3,0)两点:抛物线交y轴干点C(0,3).点D为抛物线的顶点.直线y=x-1交抛物线于点M、N两点,过线段MN上一点P作y轴的平行线交抛物线于点Q.
(1)求此抛物线的解析式及顶点D的坐标;
(2)问点P在何处时,线段PQ最长,最长为多少?
(3)设E为线段OC上的三等分点.连接EP、EQ.若EP=EQ时.求点P的坐标.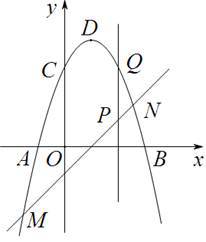
答案
(1)y=-x2+2x+3,D(1,4);
(2)点P坐标为![]() 时,PQ最大值为
时,PQ最大值为![]() ;
;
(3)P(1,0),或P(2,1)
知识点:二次函数综合题
第一步:从A、B、C三点坐标入手,代入求出二次函数表达式y=-x2+2x+3,再由表达式得到顶点D的坐标为D(1,4);
第二步:研究PQ何时最长,需要表达PQ长度,注意到P、Q两点横坐标相同,并且分别在直线和抛物线上,所以可以设P(m,m-1),Q(m,-m2+2m+3),则![]() ,所以点P坐标为
,所以点P坐标为![]() 时,PQ最大值为
时,PQ最大值为![]() ;
;
第三步:根据题目,E点可能有两个位置,E(0,1),或者E(0,2),若EP=EQ,则根据性质可知,点E的纵坐标等于P、Q纵坐标和的一半.则仍然可设P(n,n-1),Q(n,-n2+2n+3)由题意得![]() ,或
,或![]() 解得n1=1,n2=2,n3=0,n4=3,结合题意P在线段M上并且不在y轴上,所以只能取n1=1,n2=2,此时P(1,0),或P(2,1)
解得n1=1,n2=2,n3=0,n4=3,结合题意P在线段M上并且不在y轴上,所以只能取n1=1,n2=2,此时P(1,0),或P(2,1)
略








