如图1,Rt△ABC中,∠ABC=90°,BD⊥AC于点D.有结论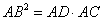 ;
;
(1)如图2,在Rt△ABC中,∠ABC=90°,点D为BC边上的点,BE⊥AD于点E,延长BE交AC于点F.若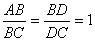 ,则
,则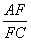 的值为( )
的值为( )
- A.
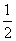
- B.2
- C.
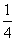
- D.4
答案
正确答案:B
知识点:相似基本模型
1.解题要点
①要求比例的值,考虑利用相似解决问题,所以过点C作CG∥BF交AD的延长线于点G,出现A字型相似,只需求出AE:EG的值即可;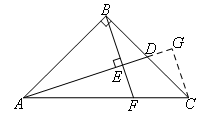
②设出比例份数,借助于题干中的结论,容易求出AE和ED,而△BED≌△CGD,
DG也能表达出来;
③利用相似对应线段成比例时要注意找准对应关系.
2.解题过程
如图,过点C作CG∥BF交AD的延长线于G
∴△AEF∽△AGC,
∴![]()
∵![]()
设BD=CD=1,则AB=2,
∵BF∥CG
∴∠EBD=∠GCD
∵∠BDE=∠CDG
∴△BDE≌△CDG(ASA)
∴![]()
在Rt△ABD中,BE⊥AD,
由题干中的结论可知:![]()
∵![]()
∴![]()
∴![]()
∴![]() .
.
略








