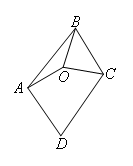
如图，已知O是四边形ABCD内一点，OA=OB=OC，∠ABC=∠ADC=70°，
则∠DAO+∠DCO=____°.

∵OA=OB=OC，
∴∠OAB=∠OBA，∠OBC=∠OCB，
∴∠OAB+∠OCB=∠OBA+∠OBC=70°，
∵四边形的内角和等于360°，
∴∠DAO+∠DCO=360°-70°-70°-70°=150°，
故答案为：150

略