（经典原题）如图，在平面直角坐标系xOy中，已知矩形OABC的两个顶点A，B的坐标分别为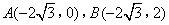．将矩形OABC沿直线AC折叠，点O落在坐标平面内的D处，若在坐标平面内存在点P，使得四边形ADOP是平行四边形，则点P的坐标为(    )

• A.
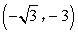
• B.
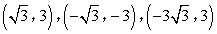
• C.
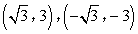
• D.

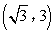
答案

正确答案：A

知识点：平行四边形的存在性  

如图，连接OD，过点D作DE⊥x轴于点E，过点O作OP∥AD，过点A作AP∥DO交直线OP于点P，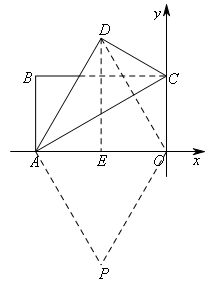

∵，四边形OABC是矩形，
∴．
∴∠CAO=30°．
由折叠AD=AO，∠DAE=2∠CAO=60°，
在Rt△DAE中，，∠DAE=60°，
∴，
∴，
∴．
∵四边形ADOP是平行四边形，

∵，
∴．
故选A．

略

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>