如图,在Rt△OAB中,∠A=90°,∠ABO=30°,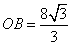 ,边AB的垂直平分线CD分别与AB,x轴,y轴交于点C,G,D.若点P是直线AB上一动点,点Q是直线CD上一动点,使得以O,D,P,Q为顶点的四边形是平行四边形的P点坐标为( )
,边AB的垂直平分线CD分别与AB,x轴,y轴交于点C,G,D.若点P是直线AB上一动点,点Q是直线CD上一动点,使得以O,D,P,Q为顶点的四边形是平行四边形的P点坐标为( )

- A.
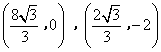
- B.
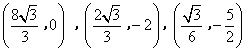
- C.
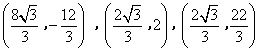
- D.

答案
正确答案:A
知识点:平行四边存在性
1.解题要点
(1)理解题意、整合信息.
根据△OAB为斜边长![]() 的含30°角的直角三角形,求出点A,C的坐标,直线AB,直线CD的解析式.
的含30°角的直角三角形,求出点A,C的坐标,直线AB,直线CD的解析式.
(2)分析特征,有序思考,设计方案.
①分析定点、动点:
O,D,P,Q为顶点的四边形是平行四边形,其中O,D为定点,P,Q为动点;
②确定分类标准:
OD为定线段,四个顶点用逗号隔开,位置不确定,定线段OD可以作为平行四边形的边,也可以作为平行四边形的对角线,分两种情况进行讨论.
(3)根据方案作出图形,有序操作.
①当OD作为边时,
根据平行四边形的判定,需满足OD∥PQ,OD=PQ,要找OD,借助平移,找出点后,设计方案,利用平移的性质,求点P的坐标;
②当OD为对角线时,
根据平行四边形的判定,需要满足OD,PQ互相平分,先找到OD的中点,根据中点坐标公式,由点P确定点Q,进而求出点P的坐标.
(4)结果检验、总结.
作图验证;分析数据,估算验证.
2.解题过程

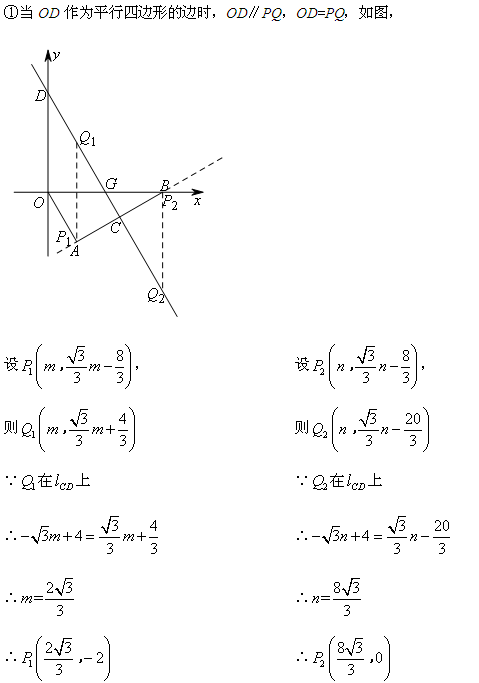

略








