（2011湖北襄阳）如图，在⊙O中，弦BC垂直于半径OA，垂足为E，D是优弧
上一点，连接BD，AD，OC，∠ADB＝30°.
（1）求∠AOC的度数；
（2）若弦BC＝6cm，求图中阴影部分的面积.
上一点，连接BD，AD，OC，∠ADB＝30°.
答案
（1）∵弦BC垂直于半径OA，
∴BE＝CE，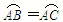
又∵∠ADB＝30°，
∴∠AOC＝60°
（2）∵BC＝6，∴
在Rt△OCE中，
∴
连接OB.
∵
∴∠BOC＝2∠AOC＝120°
∴S阴影＝S扇形OBC－S△
＝
知识点：中考热点计算
（1）由垂径定理、圆周角定理可知∠AOC=2∠ADB=60°；
（2）由垂径定理可知，∠OEC=90°，EC=3cm，又∠AOC=60°，可得
，进而可分别求出扇形OBC的面积和△BOC的面积，利用扇形面积减去△BOC面积即可得到阴影部分面积．
略
WORD格式（
