如图,在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF,求证:△DEF为等边三角形.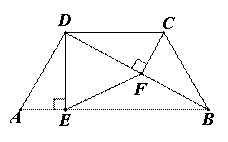
答案
证明:∵DC∥AB,AD=BC,∠A=60°,∴∠ABC=∠A=60°.∵BD平分∠ABC,∴∠ABD=∠CBD=30°.∵DC∥AB.∴∠BDC=∠ABD=30°.∴∠CBD=∠CDB,CB=CD∵CF⊥BD.∴F为BD中点.又因为DE⊥AB,∴DF=BF=EF由∠ABD=30°.得∠BDE=60°,所以△DEF为等边三角形.
知识点:中考热点几何证明
要证明一个三角形为等边三角形,通常都是先证明两条边相等,然后再证明一个角是60°.那么在这道题中,很多同学会想到通过证明三角形全等证明线段相等,也有同学想证明角度来证明两条线段相等.下面我们主要看看如何通过角度来证明线段相等.由题目可知梯形为等腰梯形,并且底角都等于60°,那么∠ABC=60°,又由BD是角平分线,可知∠DBA=∠DBC=30°,所以在Rt△DEB中,BD=2DE.又由DC∥AB,∠BDC=∠DBA=∠DBC,可知△CBD是等腰三角形,又根据等腰三角形三线合一,可知BD=2DF,进而DE=DF,再通过∠BDE=60°,可以得到三角形为等边三角形.
略








