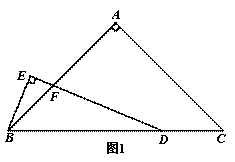
在△ABC中，∠A＝90°，点D在线段BC上，∠EDB＝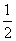
∠C，BE⊥DE，垂足为E，DE与AB相交于点F．(1)当AB＝AC时，（如图1），①∠EBF＝ °；②探究线段BE与FD的数量关系，并加以证明；（2）当AB＝kAC时（如图2），求
的值（用含k的式子表示）．
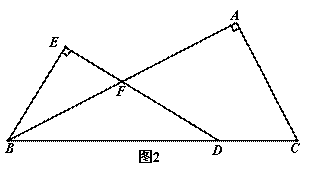
∠C，BE⊥DE，垂足为E，DE与AB相交于点F．(1)当AB＝AC时，（如图1），①∠EBF＝ °；②探究线段BE与FD的数量关系，并加以证明；（2）当AB＝kAC时（如图2），求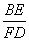
的值（用含k的式子表示）．
答案
（1）①22.5°②结论：
证明：如图1，过点D作DG∥CA，与BE的延长线相交于点G，与AB相交于点H，则∠GDB=∠C，∠BHD=∠A=90°=∠GHB
又∵DE=DE，∠DEB=∠DEG=90°∴△DEB≌△DEG∴
∵∠A=90°，AB=AC，∴∠ABC=∠C=∠GDB∴HB=HD
∵∠BED=∠BHD=90°，∠BFE=∠DFH∴∠EBF=∠HDF∴△GBH≌△FDH∴GB=FD
（2）如图2，过点D作DG∥CA，与BE的延长线相交于点G，与AB相交于点H，
同理可证△DEB≌△DEG，
,∠BHD=∠GHB=90°，∠EBF=∠HDF，∴△GBH∽△FDH
又∵DG∥CA，∴△BHD∽△BAC，
知识点：中考热点几何证明
见到题目中出现二倍角的关系以及垂直，往往想到把大角补全，作出二倍角，得到平行的关系，通过角平分线和垂直证明三线合一，进而实现线段的转移．在本题中，如果过点D作AC的平行线交BE延长线于点G，则可知△BDG为等腰三角形，进而BG=2BE，要找BE和FD的关系，可以转化为找BG和FD的关系，又可以转为证明这两条线段所在的三角形全等（第一问）或者相似（第二问），进而得出正确的结论．
略
WORD格式（
