如图，在△ABC中，∠A=50°，∠BCD=30°，∠B=∠1，求∠2的度数．

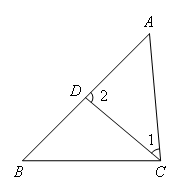
解：如图，设∠B=α，
∵∠B=∠1（已知）
∴∠1=α（等量代换）
∵∠2是△BCD的一个外角（外角的定义）
∴∠2=∠B+∠BCD（三角形的一个外角等于和它不相邻的两个内角的和）
∵∠BCD=30°（已知）
                                
∴∠2=α+30°=80°（等式的性质）
横线处应填写的过程，顺序正确的是(    )
①∵∠A=50°（已知）
∠A+∠1+∠2=180°（三角形的内角和等于180°）
②∴α=50°（等式的性质）
③∴50°+α+α+30°=180°（等量代换）
④∴∠2=α+30°（等量代换）

• A.④①③②
• B.②①④③
• C.④②①③
• D.①③④②

答案

正确答案：A

知识点：三角形内角和定理  三角形外角定理  

要求∠2的度数，有两种思路：
①从结论出发，可以把∠2看成△BCD的一个外角，
那么要求∠2，只要能求出∠B即可．
可设∠B=α，接着表达∠1，∠2，然后在△ACD中，
利用三角形的内角和等于180°求解．
②从已知出发，在△ABC中，∠B=∠1，设∠B=α，
可以利用三角形内角和等于180°求出α的度数，
然后利用三角形外角定理求出∠2的度数．
本题示范的是第一种思路．
故选A．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>