勾股图是指以直角三角形的三边为边向外作正方形构成的图案，它可以验证勾股定理．在下面的勾股图中，已知∠ACB=90°，∠BAC=35°．作△PQR使得∠R=90°，点H在边QR上，点D，E在边PR上，点G，F在边PQ上，则∠P=(    )

如图，过点A作AI⊥QR于点I，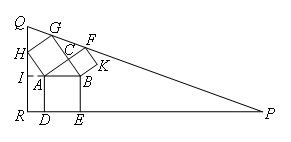

∵∠ACB=∠GCF=90°，AC=CG，BC=CF
∴△ABC≌△GFC（SAS）
∴∠CAB=∠CGF=35°
∵∠HGC=90°
∴∠HGQ=55°
∵∠BAC=35°，∠HAC=90°
∴∠HAI=55°
在Rt△AHI中可得∠AHI=35°
∵∠GHA=90°
∴∠QHG=55°
在△HGQ中，∠HGQ=55°
得∠Q=70°
在Rt△QRP中得∠P=20°
故选C

略