在△ABC中,∠ACB=90°,E是BC边上的一点,过C作CF⊥AE,垂足为F,过B作BD⊥BC,交CF的延长线于点D.若∠EAC=25°,求∠D的度数.
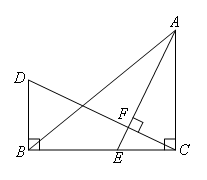
解:如图,
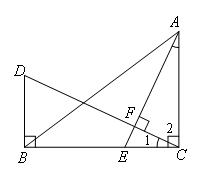
∵CF⊥AE(已知)
∴∠AFC=90°(垂直的定义)
∴∠EAC+∠2=90°(直角三角形两锐角互余)
∵∠ACB=90°
即∠1+∠2=90°(已知)
∴∠1=25°(等量代换)
∵BD⊥BC(已知)
∴∠DBC=90°(垂直的定义)
∴∠D=90°-∠1
=90°-25°
=65°(直角三角形两锐角互余)
横线处应填写的过程最恰当的是( )
- A.

- B.
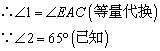
- C.

- D.

答案
正确答案:D
知识点:直角三角形两锐角互余
本题主要利用直角三角形两锐角互余和同角或等角的余角相等进行角的计算.
利用∠ACB=90°,CF⊥AE垂直互余导角可得∠1=∠EAC,结合∠EAC=25°,可得∠1=25°;在Rt△CBD中,利用直角三角形两锐角互余可得∠D的度数.
故选D.
略









