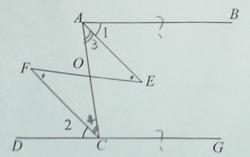
已知：如图，AC，EF相交于点O，∠E=∠F，∠1=∠2．
求证：AB∥DG．

证明：如图，

∵∠E=∠F（已知）
∴            （内错角相等，两直线平行）
∴∠3=∠4（                    ）
∵∠1=∠2（已知）
∴∠1+∠3=∠2+∠4（等式性质）
即∠BAC=∠DCA
∴            （内错角相等，两直线平行）
①AB∥DG；②AE∥CF；③两直线平行，内错角相等；
④内错角相等，两直线平行；⑤两直线平行，同位角相等．
以上空缺处依次所填正确的是(    )

要证AB∥DG，考虑同位角，内错角，同旁内角，结合题目中的已知条件，
本题利用内错角∠BAC=∠DCA．
由∠E=∠F，利用内错角相等，两直线平行，得AE∥CF（因此第一个空选②）；
进而，利用两直线平行，内错角相等，得∠3=∠4（因此第二个空选③）．
结合已知条件∠1=∠2，利用等式性质，得∠1+∠3=∠2+∠4，即∠BAC=∠DCA，再利用内错角相等，两直线平行，得AB∥DG（因此第三个空选①）．
故选C．

想一想：
1．由平行可以想什么？
2．要证平行，怎么想？
3．要求一个角的度数，我们可以怎么考虑？
 
参考答案：
1．由平行可以想同位角相等，内错角相等，同旁内角互补．
2．要证平行，找同位角、内错角、同旁内角，因为同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．
3．首先观察图形，结合已知条件，看它可以看成什么角，然后设计方案求解．如果看成三角形的内角，可以考虑通过三角形的内角和等于180°求解；如果有平行，可以考虑通过平行转移角，等等．

略