已知:如图,在△ABC中,D为BC边上一点,DF⊥AB,垂足为F,DE∥AC,∠A=∠B.
求证:∠1=∠2.

证明:如图,
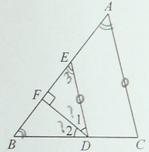
∵DE∥AC(已知)
∴∠A= (两直线平行,同位角相等)
∵∠A=∠B(已知)
∴∠B=∠3(等量代换)
∵DF⊥AB(已知)
∴∠DFE=∠DFB=90°(垂直的定义)
∴∠3+∠1=90°,∠B+∠2=90°( )
∴∠1=∠2( )
①∠1;②∠3;③垂直的性质;④直角三角形两锐角互余;
⑤等角的补角相等;⑥等角的余角相等.
以上空缺处依次所填正确的是( )
- A.①③⑥
- B.②④⑥
- C.①③⑤
- D.②④⑤
答案
正确答案:B
要证∠1=∠2,题目中有平行,考虑利用平行线的性质转移角.
由DE∥AC,利用两直线平行,同位角相等,得∠A=∠3(因此第一个空选②).
结合已知条件∠A=∠B,利用等量代换,得∠B=∠3,
由DF⊥AB,利用垂直的定义,得∠DFE=∠DFB=90°,
利用直角三角形两锐角互余,得∠3+∠1=90°,∠B+∠2=90°(因此第二个空选④).
进而利用等角的余角相等,得∠1=∠2(因此第三个空选⑥).
故选B.
略









