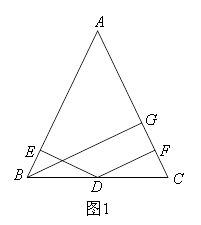
在△ABC中,AB=AC=a,BC=b,且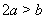 ,BG⊥AC于G,DE⊥AB于E,DF⊥AC于F.在图1中,D是BC边上的中点,则DE+DF与BG的数量关系为( )
,BG⊥AC于G,DE⊥AB于E,DF⊥AC于F.在图1中,D是BC边上的中点,则DE+DF与BG的数量关系为( )
- A.
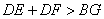
- B.
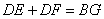
- C.
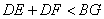
- D.无法判断
答案
正确答案:B
知识点:类比探究
1.可以根据线段关系,大胆地猜测(借助圆规、三角板等度量工具),然后验证;
2.从特征来看:中点、垂直、线段和差倍分.
(1)从中点特征出发:
①△ABC是等腰三角形,点D是BC中点,DE,DF分别垂直于AB,AC,易得DE=DF;
②DF⊥AC,BG⊥AC,则DF∥BG,又由点D是BC中点,可得DF是△BCG的中位线,BG=2DF=DE+DF.
(2)从垂直特征出发(BG,DE,DF都和垂直有关,可以考虑面积)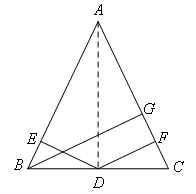
①如图,连接AD;
②根据S△ABD+S△ACD=S△ABC,可得![]() ;
;
③由AB=AC,可得DE+DF=BG.
(3)从线段结果和差倍分出发(考虑截长补短)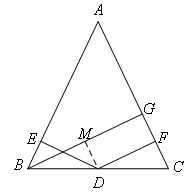
①如图,过点D作DM⊥BG于点M,则四边形DMGF为矩形,DF=GM;
②证明△BMD≌△DEB(AAS),可得BM=DE;
③BG=BM+GM=DE+DF.
故选B
略








