已知△ABC的三条边长分别为6，8，12，过△ABC任一顶点画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画(    )

设AB=6，AC=8，BC=12，如图，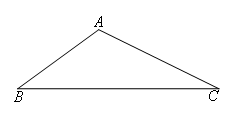

由题意，需分类讨论：
①当AB为等腰三角形的腰时，分别以A，B为圆心，AB长为半径作圆，如图，此时存在3条符合题意的直线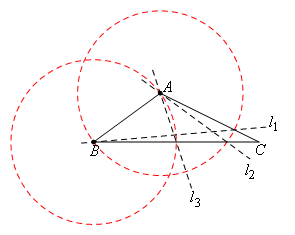


②当AB为等腰三角形的底时，作AB的垂直平分线，如图，此时存在1条符合题意的直线

③当AC为等腰三角形的腰时，分别以A，C为圆心以AC长为半径作圆，如图，此时存在1条符合题意的直线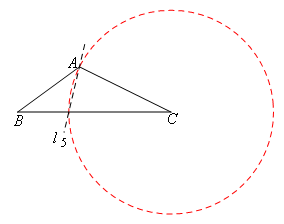

④当AC为等腰三角形的底时，作AC的垂直平分线，如图，此时存在1条符合题意的直线

⑤由题意，若BC为等腰三角形的一边，则只能作为等腰三角形的底，如图，此时存在1条符合题意的直线

综上，这样的直线最多可画7条．

略