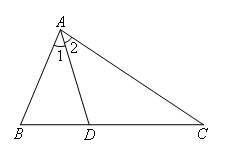
已知:如图,在△ABC中,∠1=∠2,AC=AB+BD.
求证:∠ABC=2∠C.
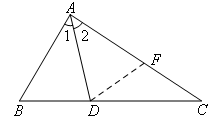
(截长法)证明:如图,在AC上截取AF=AB,连接DF.
在△ABD和△AFD中
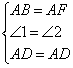
∴△ABD≌△AFD(SAS)
∴
∴CF=DF
∴∠ABC=2∠C
请你仔细观察下列序号所代表的内容:
①∠ABC=∠AFD,AB=AF;②∠ABC=∠AFD,BD=FD;③∠BDA=∠FDA,BD=FD;
④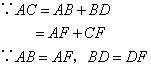 ;⑤
;⑤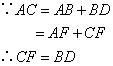 ;
;
⑥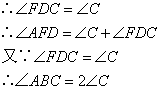 ;⑦
;⑦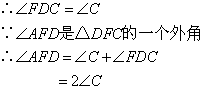 .
.
以上空缺处依次所填最恰当的是( )
- A.①⑤⑥
- B.①⑤⑦
- C.②⑤⑦
- D.①④⑥
答案
正确答案:C
知识点:三角形全等之截长补短
题中出现AC=AB+BD,这是几条线段间的数量关系,
考虑用截长补短转化成两条线段的等量关系.
这里利用截长法证∠ABC=2∠C,
考虑利用三角形全等转移边转移角证△DFC是等腰三角形,
由△ABD≌△AFD,转移边转移角得到∠ABC=∠AFD,BD=FD,
第一空应填②;
结合题中条件AC=AB+BD,可以得到CF=BD,第二空应填⑤;
得到等腰之后利用三角形的一个外角等于和它不相邻的两个内角的和
可以得到∠ABC=2∠C,第三空应填⑦.
故选C.
略









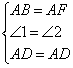
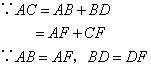 ;⑤
;⑤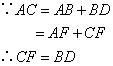 ;
;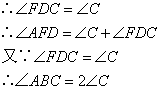 ;⑦
;⑦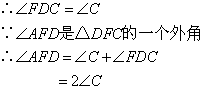 .
.