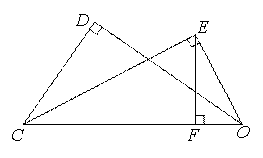
已知，如图，在△ODC中，∠D=90°，EC是∠DCO的角平分线，且OE⊥CE，过点E做EF⊥OC交OC于点F，猜想：线段EF与OD之间的数量关系，并加以证明.
答案
如图，延长OE，CD交于点G，
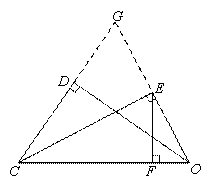
∵EC是∠DCO的角平分线
∴∠GCE=∠OCE
又∵CE=CE，∠CEG=∠CEO
∴△GCE≌△OCE
∴EO=EG，即EO=
OG
∵∠G+∠GCE=90°，∠EOF+∠OCE=90°，∠GCE=∠OCE
∴∠G=∠EOF
又∵∠GDO=∠OFE=90°
∴△GDO∽△OFE
∴
知识点：角平分线的性质
根据EC是∠DCO的角平分线，且OE⊥CE，延长OE，CD交于点G，可得△COG是等腰三角形，E是OG的中点.又根据△ODG∽△EFO，得
.
略
WORD格式（
