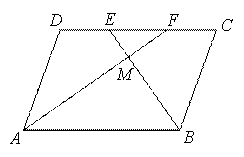
（2011湖南常德）如图，已知四边形ABCD是平行四边形.若AF、BE分别是∠DAB、∠CBA的平分线，求证：DF=EC.
答案
∵AF是∠DAB的平分线
∴∠DAF=∠BAF
又∵四边形ABCD是平行四边形
∴AB∥CD，AD=BC
∴∠DFA=∠BAF
∴∠DAF=∠DFA
∴AD=DF.
同理可证BC=EC
又∵AD=BC
∴DF=EC
知识点：角平分线的性质
由AF分别是∠DAB的平分线，DC∥AB，利用角平分线加平行线模型，得△ADF是等腰三角形，AD=DF.同理可得BC=EC.又根据AD=BC，所以DF=EC.
略
WORD格式（
