在等腰三角形ABC中，AB=AC，BG⊥AC于G，点D是BC上一点，DE⊥AB于E，DF⊥AC于F．
（1）在图1中，D是BC边的中点，试判断BG，DE，DF之间的数量关系．小明同学的思路是连接AD，借助
△ABD，△ACD，△ABC的面积之间的关系来证明．则BG，DE，DF之间的数量关系是( )
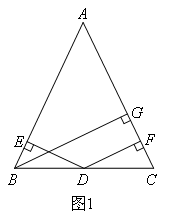
- A.DE+DF>BG
- B.DE+DF=BG
- C.DE+DF<BG
- D.无法判断
答案
正确答案：B
知识点：类比探究
可以根据线段关系，进行猜测（借助圆规、三角板等度量工具），然后验证；
从垂直特征出发（BG，DE，DF都和垂直有关，可以考虑面积），
按照小明同学的思路，借助△ABD，△ACD，△ABC的面积之间的关系来证明．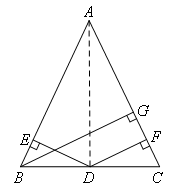
如图，连接AD，根据
，
则
，
由AB=AC，得DE+DF=BG．
故选B．
略
WORD格式（
