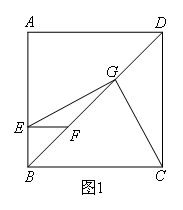
（1）如图1，在正方形ABCD的边AB上任取一点E，过点E作EF⊥AB，交BD于点F，取DF的中点G，连接EG，CG．求证：EG=CG，EG⊥CG．

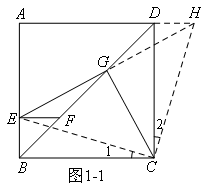
如图1-1，

下面给出了证明的路线图：

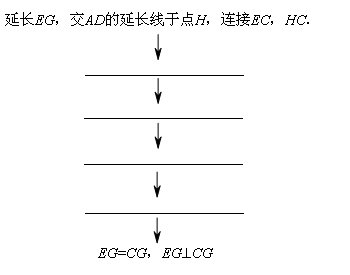
①△EFG≌△HDG；②△CBE≌△CDH；③EF=DH；④EF=DH，EG=HG；⑤EG=HG；
⑥EC=HC，∠1=∠2；⑦∠1=∠2．
以上横线处，依次所填正确的是(    )

1．解题要点
观察图形AD∥EF，点G是DF的中点，这是平行夹中点结构，
考虑延长，延长之后证全等．利用题干中给出的辅助线信息继续研究，
寻找进一步的结论来说明EG和CG之间的关系．
由“平行夹中点”证明△EFG≌△HDG，可以得到DH=EF=BE，EG=HG，
进而证明△CBE≌△CDH（SAS），可以得到△ECH是等腰直角三角形，
所以EG=CG且EG⊥CG．
2．解题过程
如图，延长EG，交AD的延长线于点H，连接EC，HC．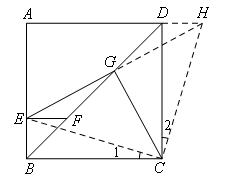

由题意得，EF∥AD，△BEF是等腰直角三角形．
∵G是DF的中点，
∴FG=DG．
∵DH∥EF，
∴，∠EFG=∠HDG，
在△EFG和△HDG中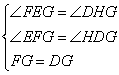

∴△EFG≌△HDG（AAS），
∴EF=HD，EG=HG．
∵EF=BE
∴BE=DH
∵BC=DC，∠EBC=∠HDC=90°，
在△CBE和△CDH中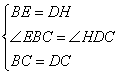

∴△CBE≌△CDH（SAS），
∴EC=HC，∠1=∠2，
∴∠ECH=∠ECD+∠2=∠ECD+∠1=90°，
∴△ECH是等腰直角三角形．
∴∠CEG=45°，
∵EG=HG，
∴EG⊥CG，
∴∠ECG=∠GEC=45°，
∴EG=CG．
所以我们的路线图是：延长EG，交AD的延长线于点H，连接EC，HC
→△EFG≌△HDG→EF=HD，EG=HG→△CBE≌△CDH→EC=HC，
∠1=∠2→EG⊥CG且EG=CG．
故选A．

略