如图,在△DAE中,∠DAE=30°,线段AE,AD的中垂线分别交直线DE于B和C两点,则
∠BAC的大小是( )
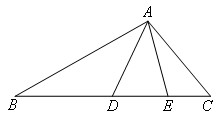
- A.100°
- B.110°
- C.120°
- D.130°
答案
正确答案:C
如图,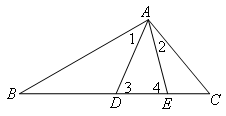
∵线段AE,AD的中垂线分别交直线DE于B,C两点,
∴BA=BE,CA=CD,
∴∠4=∠BAE,∠3=∠CAD,
即∠4=∠1+∠DAE,∠3=∠2+∠DAE,
在△ADE中,∠DAE+∠3+∠4=180°,
∴∠1+∠2+3∠DAE=180°,
即∠BAC+2∠DAE=180°,
∵∠DAE=30°,
∴∠BAC=120°.
故选C.
略








