已知：如图，在△ABC中，∠EFB+∠ADC=180°，∠1=∠2．
求证：AB∥DG．

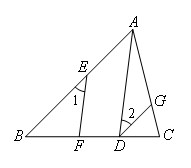
证明：如图，

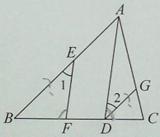
∵∠EFB+∠ADC=180°（已知）
∠ADB+∠ADC=180°（平角的定义）
∴∠EFB=∠ADB（                    ）
∴          （同位角相等，两直线平行）
∴∠1=      （两直线平行，同位角相等）
∵∠1=∠2（已知）
∴∠2=∠BAD（等量代换）
∴          （内错角相等，两直线平行）
①同角的余角相等；②同角的补角相等；③等量代换；④AB∥DG；⑤AD∥EF；⑥∠BAD；⑦∠2．
以上空缺处依次所填正确的是(    )

已知∠EFB+∠ADC=180°，由平角的定义得到∠ADB+∠ADC=180°，则∠EFB=∠ADB；
根据同位角相等，两直线平行，得AD∥EF；
由两直线平行，同位角相等，得∠1=∠BAD；
再结合已知∠1=∠2，等量代换得到∠2=∠BAD；
最后利用内错角相等，两直线平行得到AB∥DG．
第一个空：条件是∠EFB+∠ADC=180°，∠ADB+∠ADC=180°，
结论是∠EFB=∠ADB，
所以由条件得到结论的依据是同角的补角相等，②正确；
第二个空：条件是∠EFB=∠ADB，且∠EFB和∠ADB是同位角，
结合得到结论的依据是同位角相等，两直线平行，
因此应该填AD∥EF，⑤正确；
第三个空：条件是EF∥AD，得到结论的依据是两直线平行，同位角相等，
∠1和∠BAD是直线AD和直线EF被直线AB所截得到的同位角，
因此应填∠BAD，⑥正确；
第四个空：条件是∠2=∠BAD，且∠2和∠BAD是内错角，
结合得到结论的依据是内错角相等，两直线平行，
因此应填AB∥DG，④正确．
综上所述，②⑤⑥④正确，故选A．

略